図2.1第一章を参照のこと。
(1) キャパシタ、コンデンサ、蓄電器などという。容量がC[単位はファラド(farad)]のキャパシタは図2.1において
図2.1
(2-1)
あるいは
i(t) = Cdv(t)/dt (2-2)
が成り立つ２端子素子のことである。
図2-1において、キャパシタの・がついている側の電荷量をq(t)とすると
q(t) = Cv(t) (2-3)
となる。すなわち、
i(t) = dq(t)/dt (2-4)
である。
(2) 次のサイトなどが参考になる。
キャパシタ(Wikipedia)
(1) インダクタンスがL[ヘンリー]のインダクタあるいはコイルとは、図2-2において
図2-2
v(t) = Ldi(t)/dt (2-5)
または
(2-6)
が成り立つ２端子素子をいう。電流i(t)がつくる鎖交磁束(linkage flux)をφ(t)とすると
φ(t) = Li(t) (2-7)
v(t) = dφ(t)/dt (2-8)
が成り立つ。φはファイと発音する。
(2) 次のサイトなどが参考になる。
キャパシタとインダクタ(pdf)
Self-Inductance and Inductive Reactance
(1) 図2-3のような一次コイル、２時コイルの自己インダクタンスがそれぞれ
と
で両コイル間の相互インダクタンスがMの変成器あるいは変圧器（トランス)は端子電圧、電流の間にM>0として
図2-3
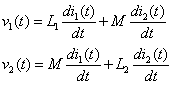(2-7)
が成り立つ素子をいう。図2-3のドットは図のような方向に電圧と電流の向きをつけたとき、M>0として式(2-7)が成立することと約束する。
(2) 一方、次の図2-4のようにドットをつけたときは、M>0として、
図のように電圧と電流の向きを決めたとき
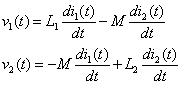(2-8)
が成り立つことを意味する。
(3) もし、ドットが書き込まれていない、変成器があったときは、図2-3の極性であるとする。
(4) 加極性接続 教科書p.27
(5) 減極性接続 教科書p.28
(6) 次のサイトが参考になる。
(1) 抵抗
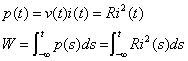(2-9)
(2) キャパシタ
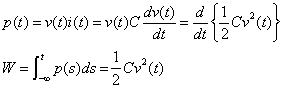(2-10)
(3) インダクタ
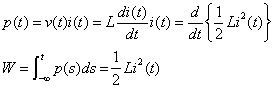(2-11)
(4) 変成器
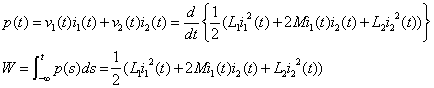(2-12)
問 式(2-12)からW >= 0 となるためには
(2-13)
が必要十分となることを示せ。
©大石進一